\renewcommand{\item}{\nitem}

Planned Outline, In-Person Meeting 2

  1. Syllabus Location

  2. Review

  3. Q&A

  4. Midterm

  5. HBS Case

  6. Purposes of markets and firms

  7. Open questions

Syllabus – Covered Already

Week Date Topic
1 03/27-04/05 Ch 02-03: NPV, Terminal Values, Loans
2 04/07-04/09 Ch 04-05: Capital Budgeting, Treasuries, Term Structures
* 04/11 Introduction, Q&A, Mini-Exam, Project Start
3 04/14-04/19 Review, Catchup, Realignment
4 04/21-04/26 Ch 06: Risk, Debt+Equity
5 04/28-05/03 Ch 07: Asset Classes (short); Ch 08: Portfolios
6 05/05-05/10 Ch 10: CAPM, Market

Syllabus – Next Weeks

Week Date Topic
* 05/09 Review. Homeworks. Midterm. In-Class
7 05/12-05/17 Ch 11-12: Imperfect Markets, Efficient Markets
8 05/19-05/24 Ch 13: NPV Pitfalls, Strategy
9 05/26-05/30 Ch 14: Financial Statements
* 05/30 Review. Homeworks. In-Class (maybe final)
10 06/02-06/07 Ch 15: Comparables, Financial Ratios
11 06/1? Maybe Final

AI use damages professional reputation, study suggests.

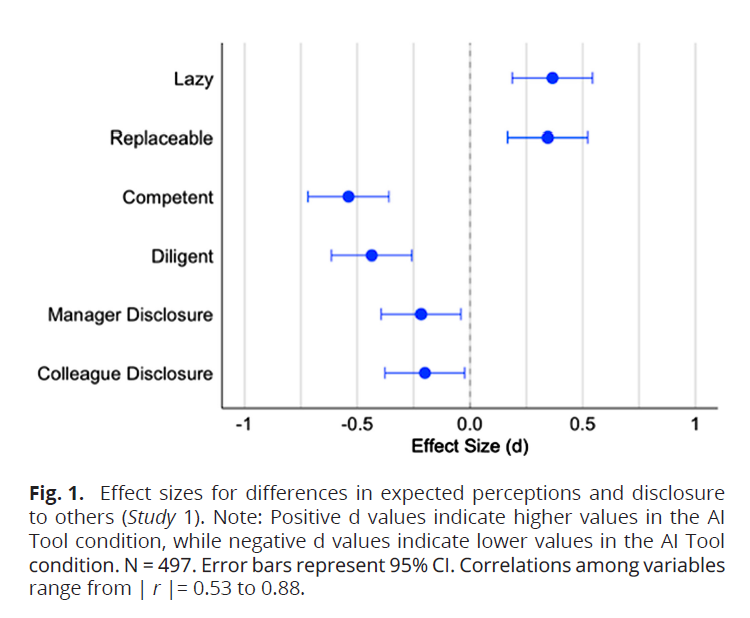{ width=75% }

  • Why Learn Finance? Why Not Just ChatGPT? Integration!

Course Review

\Large

So Far

  • Beware interest quotes

    • For exams, pick what you consider to be the most reasonable rate. If my question seems halfway ambiguous, just state “I am assuming this rate is the true annual rate; if I assume it is just a quote, I would use x%” or “I am assuming this rate is just an annual quote, so I divided by 12; if I assumed it is a true interest rate, I would use $(1+x\%)^(1/12)$”. You will of course get full credit.
    • In the real world, interest rates vs. interest quotes are a true mine field. (Only the simplest of bank rates are most standardized.)

\clearpage

  • Rates of Returns: Compounding, Annualizing

    • $r = (P_1 - P_0)/P_0 = P_1/P_0 - 1 \quad\Leftrightarrow\quad 1+r = P_1/P_0$

    • Ex: 2x = 100%; 1.5x = 50%; 0.9x = –10%.

    • Ex: if first 1.5x, then again 1.5x: you get 2.25x.

      • $(1+50\%)\cdot(1+50\%) = (1+125\%)$

    • Ex: if first 1.2x, then 0.7x (0.7x means lose 30%, i.e. -30%):

      • $1 to $1.20 to $0.84. (Or $250 to $300 to $210.)

      • $(1+20\%)\cdot(1+(-30\%)) = 0.84 = (1+(-16\%))$.

    • Ex: Annualizing: What $x$ in $(1+x)^2 = (1+(-16\%))$?

      • like $\Rightarrow (1+x) = (1+(-16\%))^{1/2} = 0.9165$.
      • like $\Rightarrow x\approx 0.9165-1 \approx (-0.0835)\approx-8.35\%$.
      • This is the annualized rate of return (think “as if average constant speed or rate”)

\clearpage

  • Three Versions: \((1+r_{0,2}) = (1+r_{0,1})\cdot(1+r_{1,2}) = (1+r_{\bar2})^2\)

    • Holding rate of return is compounded interim holding rates of return or compounded annualized rate.

\clearpage

  • Present Value PV

    \(PV= \frac{c_1}{1+r_{0,1}} + \frac{c_2}{ 1+r_{0,2} } + \frac{c_3}{ 1+r_{0,3} } + ...\) \(PV= \frac{c_1}{1+r_{\bar1}} + \frac{c_2}{(1+r_{\bar2})^2} +\frac{c_3}{(1+r_{\bar3})^3} + ...\)

    • Discount rate: the $r$ here.

    • Always think of r in this context as the “opportunity cost of capital,” i.e., what you could get in another equivalent project elsewhere in the economy.

    • Discount factor: the $1/(1+r)$, that multiplies a future dollar into its equivalent today.

  • NPV \(NPV= -c_0 + PV\)

    • really, just making sure you have the upfront cost included.

\clearpage

  • Terminal Value (perpetuity with constant growth):

    \[PV= \frac{C_1}{r-g}\]
    • Hugely important in pro-formas as standin for exp sales price.
    • In Gordon Dividend Growth model and equivalent earnings models
      • Intuition on why some firms have higher $D/P$ and $E/P$ ratios.
      • E and D replace C
    • Often used to assess (badly) “value” of stock market and/or its expected $r-g$.

\clearpage

  • Loans

    \[\mbox{Loan Amount} = \frac{\mbox{Payment}}{r} \cdot \left[ 1 - \left(\frac{1}{1+r}\right)^T \right]\]
    • Make sure to know correct $r$ and $T$, often monthly.
    • First loan payment: always next month.
    • Comparing loans, leases, etc., with different upfront payments

\clearpage

  • Internal Rate of Return

    • Generalizes rate of return to more than two periods.
    • Find numerically by solving $NPV(\, r\, ) = 0$ for r.
    • Not to be calculated in full on any exam.

\clearpage

  • Term Structure of Interest Rates

    • Annualized rates of return are term-dependent.
    • Treasury Yield Curve
    • Big deal in the real world.
    • No free money from term-structure slopes!
    • Also practices return and NPV calculations with real-world generality.
    • (Signaled economic future in the past.)

\clearpage

  • Random Values

    • An RV is a “histogram,” a placeholder for such (and usable as algebraic variables)
    • Roulette vs. History. Is history a trustworthy guide?

  • Risk Aversion and Financial Markets’ Raison d’Etre

    • you like mean; you don’t like risk.

  • Expected reward and risk calculations

    • Mean, Variance, Standard Deviation
    • Calculate from first principles (probabilities conceptually)
    • Typically, estimated (sampled) from historical data in economics.

\clearpage

  • Debt and Equity

    • Key building blocks of finance.
    • Not “partner-like” shares, but different contingent payoffs.
      • e.g., you get 10%, I get 90%.
    • Splits projects into safer and riskier components for different buyers.
      • Implications for risk and reward
    • Exercise soon.

\clearpage

  • Portfolio Statistics

    • A portfolio is a list of investment weights.
    • A portfolio rate of return is a weighted sum of investment rates of return.
    • Ex: You buy $8,000 worth of M and $2,000 worth of T. Then \(r_P = 80\%\cdot r_M + 20\%\cdot r_T\)

  • Portfolio Expected Return

    • Expectations of linear sums were taught in statistics.
    • Expected return is linear: $E(w_x\cdot x + w_y\cdot y) = w_x\cdot E(x) + w_y\cdot E(y)$
    • \[E(r_P) = E(80\%\cdot r_M + 20\%\cdot r_T) = 80\%\cdot E(r_M) + 20\%\cdot E(r_T)\]

\clearpage

  • Portfolio Variance and Standard Deviation

    • Not linear: $Var(x) + Var(y) \neq Var(x+y)$
    • $Var(w_x\cdot x + w_y\cdot y) = w_x^2\cdot Var(x) + w_y^2\cdot Var(y) + 2\cdot w_x\cdot w_y \cdot Cov(x,y)$
    • \[Var( r_P ) = Var(80\%\cdot r_{M} + 20\%\cdot r_{T}) = .64\cdot Var(r_M) + .04\cdot Var(r_T) + .32 \cdot Cov(r_M,r_T)\]
    • You need not memorize the weighted formula…but you must be aware of it. A “covariance” term matters!

  • Covariances

    • When adding a little of asset T to your portfolio, the covariance is typically a bigger deal than T’s own variance.
    • Because we care about risk, lots of finance revolves around covariances.

\clearpage

  • Portfolio diversification and market beta

    • Works because of this non-linearity of variances and standard deviations

    • Works because of covariances. (If covariances are very high, like one share of TSLA and another share of TSLA, there is no diversification.)

\clearpage

  • Do you dislike standard deviation or market-beta?

    • Q: Do you prefer a portfolio with low market-beta or low standard deviation?

    • A: You prefer a portfolio with low standard deviation.

    • You don’t care about the overall market-beta of your portfolio.
    • However, when forming your portfolio, you can form a lower-standard deviation portfolio by buying (a) a highly diversified portfolio, and (b) “tilting” more towards individual low-beta stocks. Then, as to (b), if the rest of your (market-like) portfolio goes down, your low-beta stocks don’t go down so much and “rescue it.”
    • You don’t hate high beta stocks intrinsically; you hate them only when/because they make your overall portfolio standard deviation worse.

\clearpage

  • Thought Experiment: Imagine a single stock that has both a huge standard deviation and a huge negative market beta.
    • Q: In this case, ceteris paribus, would you like to hold a portfolio consisting only of this stock?
    • Q: In this case, ceteris paribus, would you like to completely avoid sticking this stock into your portfolio?

  • Intuition: Think of neg beta stocks like “salt”?? (and pos beta stocks like poison)

    • A little salt is good, helping your overall meal.
    • All salt is terrible (well, useless for pfio sd)

  • Intuition: Lower or Negative beta is like insurance

    • Would you invest all your money into house insurance?

\clearpage

  • Covered “basic informative background about US financial market history”

    • Risk and reward of stocks, bonds, cash.
    • Some examples of non-synchronicity and market-betas
    • Market beta is \(\beta_{i,m} = \frac{cov(r_i,r_m)}{var(r_m)}\)
    • similar to correlation (sign always identical)
    • PS: sort of part of the above portfolio return variance formula

\clearpage

  • CAPM

    • We cover the most basic theory and application \(E(r_i) = r_f + [ E(r_m) - r_f ]\cdot \beta_i\) $r_f$ and $E(r_m)-r_f$ are economy wide constants. Only the firm’s market-beta determines the firm’s expected rate of return. Higher beta-stocks need to offer higher expected rates of return, or no one would like them.
    • The CAPM is also called the “SML” (securities market line).
    • It is “best practice,” overwhelmingly used in the real world.

Near Future

  • Future (To Be Covered)

    • The Ugly of the CAPM: “Bad Practice”

    • Market Perfection and Market Efficiency

      • Entrepreneurial Finance

      • Hurdle rates vs. Expected returns

    • “Easy Money”: BTC? Vanguard?

    • “Super-Practical Capital Budgeting Problems”

    • Financial Statements [such as working capital, accruals, and cash flows]

    • Comps and financial ratios.

Solving Some Questions

  • Thanks, Caitlin.

Midterm, 90 minutes

HBS Case

Two Choices

  1. Match My Doll Clothing

  2. Design Your Own Doll

Covered in this Case:

Coverage Topic
Yes Ch 02-03: NPV, Terminal Values, Loans
Yes Ch 04-05: Capital Budgeting, IRR
Implied Ch 06: Risk, Debt+Equity
Implied Ch 10: CAPM, Market
Partly Ch 11-12: Imperfect/Efficient Markets: One project only
Partly Ch 13: NPV Pitfalls, Strategy
Yes Ch 14: Financial Statements
Yes Ch 15: Comparables, Financial Ratios
Yes Ch 21: Pro Formas

Not Covered in this Case:

Coverage Topic
– Ch 04-05: Treasuries, Term Structures
– Ch 07-09: Asset Classes , Portfolio Formation
– Ch 20: Payout Policy

Covered in Future Classes

  • We have too much to cover to allow us to teach the key concepts of finance embedded in cases. The UCLA Anderson finance elective should recap almost everything we do, but in longer HBS case format.

  • The real “fun” part would have been not a “fake HBS scenario”, but the cancelled course project, which was to put together a real-estate project pro forma.

In-Class Discussion

  • Is risk aversion (disliking standard deviation of overall pfio) plausible?

  • Why do financial markets exist in the first place?

  • Why do firms exist in the first place?

  • Preview: Internal Capital Budgeting with imperfect information

  • Preview: Common Mistakes and Overconfidence

Open Questions